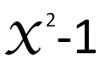exploring the undesigned
intelligence of the numberverse
lists/generators: Perfect Squares, Composites, Primes
About This Site
Natural Numbers is my personal exploration into number theory. It is autodidactic, and it is iconoclastic. It is factual, and it is speculative. It is not recommended for footnotes!
- Michael M. Ross
It's out there...
The Twin-Prime Conjecture
"My personal proofs"
The numbers are here...
"...out all day long.
All day long,
it goes on and on"
The First 1,000,000...
Generate Your Own Up to 1027...
Experimental Calculators
ZetaTest:
Infinite series
MinusSquare: Factoring
FermaticTest:
Probable prime
QTest:
Quadratic Series
RadiusTest:
Spiral lines and curves
PrimeTest
Analysis
Miller-Rabin:
Demonstration
Secrets of the Spiral
Proximate-Prime Polynomials
A proximate-prime polynomial is simply a quadratic equation - a finite polynomial of the second degree - that is derived from four successive (proximate, or neighboring) primes. Proximate-prime polynomials are interesting because they exhibit much greater prime densities than other polynomials.
The high primality of prime-derived quadratic sequences
What is a
"perfect prime polynomial"?
What is polynomial pronic
alignment?
Use an Excel spreadsheet to explore polynomial primes!
Catch the Wave...
When you graph primes against an X-axis that treats the expanding interval between successive perfect squares as a constant unit subdivided into equal parts, you produce a distinctive wave form for primes and prime factors.
Try out an ingenious Excel worksheet to see the wave!
Counting primes by quadratic interval
Fixing Fermat’s Factorization Method
How do you make Fermat's method of factorization faster than trial division...?
The Magic Square of Subtraction...
For every composite number that is not itself a perfect square there exists a pair of nonconsecutive perfect squares whose difference is equal to the composite. Even before we get to the subject of factorization, the consequences of this observation are fascinating and far-reaching.
Part
1 - A 'Classic Discovery'
Part 2 - A
Deterministic Test
Q-Paired Primes...
It began with an exploration of biquadratic paired primes: 2 primes separated by the equivalent of exactly 2 quadratic intervals.... Then the investigation took the logical next level by asking the question: Are there prime pairs that are separated by other, greater multiples of the quadratic interval? And if there are, what are the frequency characteristics by interval size and perfect square offset? The results are in, with charts, an Excel visualization, and masses of half-digested data...!
Read about the latest
findings
What are Biquadratic Paired
Primes?
Two "new" rules of perfect squares
How I learned not to be
afraid of big numbers
It's a question of
magnitude...
Using Excel as a tool for number theory
Find examples throughout this site that demonstrate using VBA code with worksheets and graphing - including generating primes, perfect squares, and composites, doing modular arithmetic, calculating GCDs, and more....
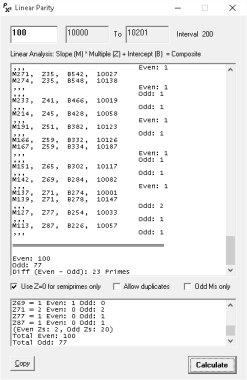
This is a legacy site. I'm leaving it up for some useful material that has thousands of external backlinks. These days, I post most of my math ideas on Quora.November 20, 2015 Legendre’s Conjecture Is Doubly True Constructing a Parity Truth Table for the Interval Between Perfect SquaresFor a quadratic interval there can be no bijective function between the set of odd numbers in the interval and the set of solutions for linear equations with odd slopes in the interval. A PROOF BY PARITY For a set of linear equations whose solutions are every composite \(y\) between \(x^2\) and \((x+1)^2\), if the intercept of each slope is \(b=2m\) and there is one odd slope for which \(2m+b\) is an even \(y\), there must be one fewer odd than even \(y\)s in the interval. Every composite number can be a value of a slope-intercept equation for a straight line. For the interval between two perfect squares, \(x^2\) and \((x+1)^2\), the size of the set of intersecting slopes is equal to \((x+1)\cdot2\). The linear equations are of the standard form \(y= mz+b\) where the intercept is double the slope (\(b = 2m\)). By definition, \(m\) is a factor - prime or composite - of \(y\). Of a set, the smallest \(m\) is \(x+1\) and the largest \(m\) is \(\frac{(x+1)^2}{3}\). There are no other slopes required to intersect every nonprime number in the interval with the exception of semiprimes divisible by \(2\) - that is, \(y\) = \(b\). Discard the slopes for which \(m\) is even. Of interest are odd-\(m\) slopes that intersect odd and even numbers where the value of \(y\) can only be even within a perfect square interval. Where \(m\) is odd, the value of \(y\) is the same parity as \(z\). Therefore: for \(z=0\), \(y\) is even (\(y=b\)); for \(z=1\), \(y\) is odd (\(y=m+b\)); for \(z=2\), \(y\) is even (\(y=2m+b\)). Every interval greater than \(\{36,49\}\) has at least two slopes where: for \(z=1\), \(y < x^2\); for \(z=2\), \(y > x^2\) and \( < (x+1)^2\); for \(z=3\), \(y>(x+1)^2\). Equivalently, there are at least two composites of the form \(2\cdot2\cdot m\) where \(m\) is odd. Notice that an odd-\(2m\) slope can cross just one number in the interval. An odd-\(m\) slope can have two \(y\) values (odd and even) only if it has variables \(z\) and \(z+1\) where \(z>\frac{x}{2}\). The absence of odd numbers on the two aforementioned slopes within the interval means that, for the set of linear equations whose values are all the composite numbers between \(x^2\) and \((x+1)^2\), two fewer odd than even numbers are intersected. These nonintersected numbers are absent from every other slope also. Since every composite is intersected by two or more slopes (one for each prime factor), the two odd numbers that are not intersected by any slope can only be primes. This is true for every perfect square interval. 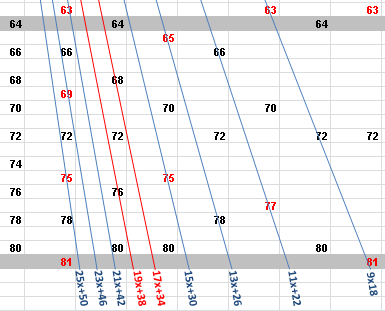
Illustrates the odd-\(m\) slopes for \(\{64,81\}\)
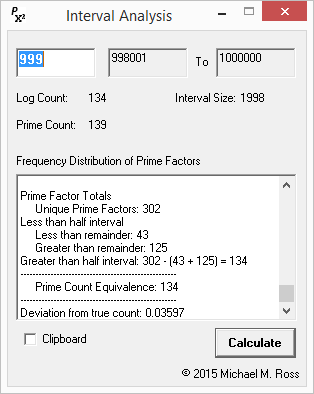
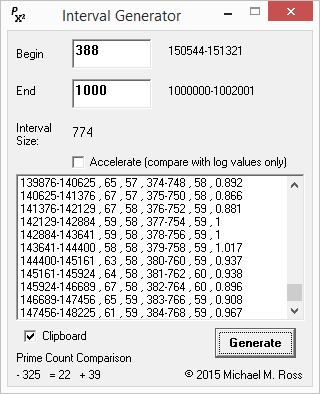
March 23, 2015 Is the Prime Count of x to 2x a Lower Bound for Prime Count x2 to (x+1)2?
Nearly. Given any even span of integers, the number of primes greater than half the span is nearly equivalent to the prime count between the square numbers for which this integer span is an interval. For the first 20,000 perfect square intervals, the average value of the "half-interval count" is 0.952 of the true prime count. The half-interval count is just under the true prime count for 97.6% of intervals, is the same as it for 0.4%, and is just above it for 2.0%. It is also converging. Download data (784KB)
There's a small cognitive leap you need to make in order to understand the significance of this near equivalency. The primes that are greater than x and less than 2x are also prime factors within the span's corresponding interval between two perfect squares. But these primes cannot be the smallest prime factors in the composites of x2 to (x+1)2. Smallest is highly significant; you will have to read the explanation below to understand why. If the half-interval count is a watertight lower bound above a certain magnitude - as it appears to be - that fact leads directly to proving Legendre's Conjecture: Given the Bertrand–Chebyshev theorem (n < p < 2n), the correlation of the prime counts for n to 2n and n2 to (n+1)2 proves "There is a prime number between n2 and (n+1)2 for every positive integer n." I have two small programs: one illustrates how it works, the other illustrates how well it works. (You can graph the CSV data with Excel.)
. . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
December 2, 2014 The Trivial Factors of X2-1
An interesting property of even perfect squares minus 1 (which are always composite) is the triviality of their smallest prime factor unless they are twin-prime composites. This makes it extremely fast to factor them and easy to determine the instances of twin primes (simply by elimination). The rule is that the smallest prime factor of a non-twin-prime X2-1 composite cannot be greater than the square root of its square root - and usually much smaller. If such a factor is not found, the composite must be the product of twin primes. Thus the largest of these non-twin-prime factors less than 1012 is 991 for 999836006723. Here is the complete list of the odd X2-1 composites less than 1012 with their smallest prime factor (including the twin primes): Zipped-up CSV file (2.6MB). . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
November 21, 2014 Superfast Twin-Prime Generator for Excel Download Twin-Prime Generator I've written a lot about twin primes and why the conjecture can be considered already proved by the Infinitude of Primes and the Fundamental Theorem of Arithmetic. This Excel program gets its speed by exploiting the universal property of all twin primes:
In other words: Don't look for primes! Look for one tiny class of semiprimes. The product of all twin primes is an even perfect square minus 1. And since we're searching for semiprimes, a primality test is not required. Any factor (prime or not) less than the square root of X2 - 1 eliminates the composite as a candidate. Furthermore, these factors are usually trivial - that is, they're found long before X. The complete predictability of the product location and the elimination of a primality test account for the polynomial speed of this algorithm. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
November 14, 2014 Fractional Elimination of Prime Factors, Perfected! Download Demonstration Program Well, almost perfected.... My fractional-elimination algorithm produces an arrow that pierces the heart of the primes for the intervals I've graphed. (Straying to the north for intervals a few magnitudes larger is a possibility based on some limited sampling. However, I'll let the graph speak for itself.) 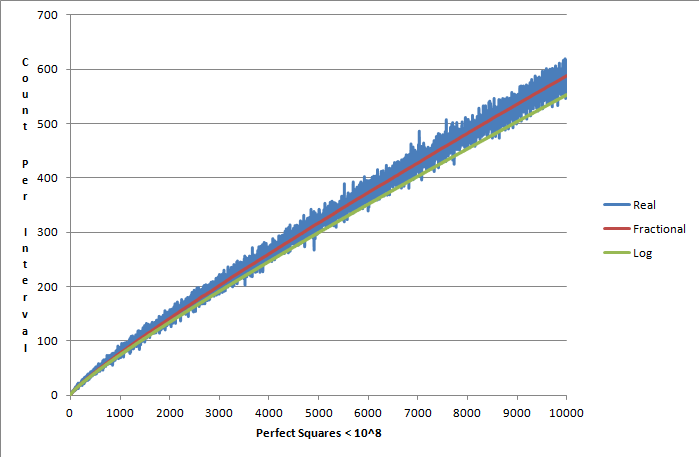
Download the data (Excel worksheet) (340KB) So what is the extra step that makes this work so beautifully? The fractional prime-counting algorithm now takes into account the "unpredictable", or more correctly probabilistic, occurrence of prime factors greater than half the interval (which I noted in my previous post). These factors must appear once, but can occur more than once. The new step in the algorithm is to apply simple logic to this, by extending fractional elimination with fractional division. Taking the case of 81 -100 = 19, half the interval is 9.5. The primes greater than half are 11, 13, 17, and 19. It's easier to think backward: Since the interval is 19, 19 can only be a prime factor once. Now consider 17: It has a 17/19th possibility of occurring more than once. Knowing nothing about the factors in this prime interval, if 17 was a factor of the 1st or 2nd composite in the interval, it would occur again in the 18th or 19th composite. With this understood, we can now express a weighted, hypothetical version of 17, which is 15.21. And so on....
The modified algorithm is as follows:
Repeating this for every interval produces a picture-perfect primes-per-interval curve. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . . November 7, 2014 A Prime Growth Function: A Curve That Counts Unlike the "asymptotic law of the distribution of prime numbers", the curve that I have graphed using the method of fractional elimination of prime factors (see how the formula works) is generated by a calculated value for every quadratic interval. The importance of this is that, unlike the asymptotic curve, this curve is the product of a discrete function applied to every perfect square interval, and it shows the growth in the prime count is due to the rules of arithmetic that apply to every interval (independently of every other interval). 
The line is almost a mirror-image of x/log x. It's actually slightly more accurate than the asymptotic curve for this data range, in that the real prime count crosses the "fractional curve" with higher frequency. Why is it not an exact representation of the true prime-counting growth rate? The explanation is that the prime factors greater than the interval's midpoint can be represented once or more than once depending on how the cards fall. Substitute composite for card, and you will understand it's a stochastic process without applying a lot of computational effort to it. (That would miss the point anyway.) For the baby case of interval {81,100}, for example, 11 occurs twice, but 13 and 17 occur only once. Hypothetically, either 13 or 17 could occur twice in the interval because they are smaller than it. Fractional elimination "assumes" that every integer appears "as a fraction" n divided by the remaining interval. Since these are fractions and not whole numbers, the result cannot be perfect. Download the data (Excel worksheet) (521KB) . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
November 1, 2014 Toward Setting a Lower Bound on the Quadratic Prime Count . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
October 20, 2014 "Legendre's by Lego": It's Geometry! There is a simple geometric principle that demonstrates primality and symmetry are equivalent properties in every perfect square interval. Specifically, it relates to the lines of symmetry of quadrilateral shapes. Imagine you're making squares with counters or Lego pieces or whatever. Begin with a 2-by-2 square. You're allowed to put down only one piece at a time by adding each one to the existing shape. So you're first task is to get from 2-by-2 to 3-by-3. Can you do this while keeping the shape a rectangle? You can change the shape with each new piece you put down but only to another rectangular shape. (Don't get creative: You must keep the distance between each adjacent piece the same.) Let's just try it: It becomes clear right away that with certain odd numbers you cannot keep the shape rectangular. These are prime numbers. The rule is simple: You cannot add counters to make one perfect square into the next bigger perfect square - 2*2 to 3*3 or 10*10 to 11*11 - and maintain rectangular symmetry with every addition. Specifically, the squares have two lines of symmetry. When you add "composite counters", the rectangle has one line of symmetry. When you add "prime counters", you break the rectangular symmetry. Exactly what does this mean for the distribution of primes in perfect square intervals? For every perfect square interval there is one pronic number (also called a rectangular or oblong number). Pronic numbers have a couple of interesting properties, but the one we're interested in here is that they lie at the midpoint of every perfect square interval: x(x+1): The sequence begins: 2, 6, 12, 20, 30, 42. They are always even (and, therefore, apart from 2 always composite). (Just to be clear, the pronics are not the only numbers that I'm loosely calling rectangular. However, they are "special". They occur only once in every interval, and they are always the same "shape".) Now visualize the pronics: A rectangle with dimensions determined by two consecutive integers (for example, 2*3 or 10*11). These dimensions are the square roots of the squares that they "divide". It is morphologically impossible to change a square to a pronic in increments of one without an intermediate asymmetry. Between x2 and x(x+1) there must be one asymmetry - or prime number. Between x(x+1) and the next x2 there must be one asymmetry - or prime number. Therefore, there must be at least two primes per perfect square interval. We did not have to wait 220 years for this truth, but essentially that's what the story is. It does not rest upon the Prime Number Theorem; it does not rest upon the Riemann Hypothesis. It rests upon geometry, although whether or not a geometer can prove that is another question. The Ross Conjecture: "It is impossible to change a square of countable units to a pronic of countable units in increments of one without an intermediate asymmetry." . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
October 12, 2014 A Formula for Counting Primes in Quadratic Intervals Yes. Why not?
Presto! Example Take the square interval 81 - 100 = 19. Apply division and subtraction as follows:
There are three primes between 81 and 100: 83, 89, 97. Why does this work? Simple:
I've created a small program (for Windows) to demonstrate the algorithm. Predict Primes Per Interval (9KB) Conclusion: If it can be shown that this method of elimination is valid, it can be used toward a proof of Legendre's Conjecture. For example, it suggests a proof by contradiction as follows:
That would be an impossible result. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
September 10, 2014 Are the "Landau problems" really one problem? Four green bottles hanging on the wall, Landau's problems are four conjectures of number theory that were stated by Edmund Landau to be "unattackable at the present state of science" 102 years ago. One thing can be said for certain about Landau's problems: What a sad state of affairs! What other scientific discipline would tolerate the humiliation of such a situation for 102 years? The working hypotheses must be that all four are true based upon all the available evidence. Yet for number theorists, a hypothesis is no more than a hunch. These four conjectures are in the deadbeat category of unproved, and they could remain there for infinity employing many able mathematicians. Why? Because academic mathematicians are concerned with infinity, and a proof must be deterministically true to infinity. Such proofs are extremely elusive, if not impossible, for any conjecture that depends on prime number distribution that is more strictly defined than asymptotically. Because academic mathematicians do not have deterministic knowledge about prime numbers, the Prime Number Theorem, also called the "asymptotic law of the distribution of prime numbers" is the best they can do: a trend that's proven but still probabilistic - and, honestly, not that interesting. (Even the holy grail of deterministically proving the Riemann Hypothesis will only refine this trend. Despite the enormous amount of attention the RH gets, it's essentially geeky. It will not provide a deterministic solution to the prediction of prime numbers. It will simply refine the PNT.) Yet we know, from very first counting principles, that every prime number is accountable for merely by the rules of arithmetic. It's only that mathematicians will never be granted the computational power to apply those rules of arithmetic to infinity - or even close! Do you remember that one about the permutations of a standard deck of playing cards? The factorial of 52. If we consider each playing card to be a prime number, those primes would account for 52! composites. That is 80658175170943878571660636856403766975289505440883277824000000000000 different composites with distinct factors. Imagine counting them. (By comparison, the age of the universe in seconds is about 432043200000000000.) Well you get the idea. However, what really makes the Landau problems problematic is not the limitations of computational power, but the limitations of number theory. Number theory, or higher arithmetic, is the study of integers. It's a collection of "magic tricks" that enable mathematicians to manipulate and understand big numbers more easily. However, there appears to be one thing that's missing from that box of tricks: A means to relate the quadratic growth of square numbers with the asymptotic growth of prime numbers. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
My thumbnail thesis is that starting about 150 years ago, academic mathematics began to lose touch with the bedrock principles of the Infinitude of Primes and the Fundamental Theorem of Arithmetic out of lack of things to do. About the same time, some overlooked classical problems also reemerged, such as the twin-prime observation. Because of their late arrival, the Landau problems were caught between Euler's ordinal universe and Cantor's cardinal universe. Then add to that the parallel universes of complex numbers and planes, combinatorics and topologies, probability and statistics, computer logic and algebra - the whole panoply of the mathematical sciences. I suggest that the Landau problems are really one problem. The inability to call them proven with the current standard of academic rigor - despite their obvious, overwhelming, likelihood of being true - is because of the following:
1. They've stood for over a century, so it's assumed they must be intractable. I add to these three two other reasons of the cosmic joke variety:
4. One of these is quite possibly provable by arithmetic or algebra without needing any advanced concepts or techniques. * This has created a logjam. Things that are easily observable - and for which a possibility of error approaches the infinitesimally tiny - are ignored. And yet, if you step back it's quite silly to say that you cannot admit something as true until it is proved that not a single exception to it will be found until infinity. That's an absurdist point of view if you think about it. Human beings are heuristic beings, and even mathematicians are not permitted firsthand knowledge of infinity. We have to imagine it. It seems to me that some, not all, mathematicians are not pattern-seekers but think atomistically and linearly. That's fine - if there is authenticity (and even originality)! For me, there are more interesting ways to understand the natural numbers than the classical model in which they march, like little tin soldiers, to infinity on a line. My mental-model is cyclicality around a geometric backbone. I subscribe to the philosophy of holism (from the Greek holos). My only faith is that natural systems taken as a whole have properties that cannot be understood only in terms of their component parts. Thus, "The whole exists prior to and is more elementary than its parts." . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
* I refer to one and the same problem: Legendre's conjecture. It is clearly and demonstrably true - and has been since the time Legendre and Euler lived. Wikipedia states, matter-of-factly without irony and without attribution: "a counterexample near 10^18 would require a prime gap fifty million times the size of the average gap." Such a counterexample will never be found. If it were found, the Prime Number Theorem would, ipso facto, be proved false. In reality, the number of primes between perfect squares increases indefinitely and absolutely with minor perturbations that never exceed a known error limit because the quadratic growth of square numbers "more than negates" the decline in the density of primes. And I will explain why the PNT may be admitted as proof of this. Because the three other Landau problems are closely interconnected with this one, if this one falls - that is, is stamped with a credible seal of a proof - the other, harder ones, become less intimidating and more vulnerable to attack (academic math lingo for being provable). A common response a mathematician will make when presented with the facts of Legendre's conjecture is something like this: The PNT cannot be used to prove Legendre's conjecture because the PNT is an asymptotic law that's a discrete limit applied to all the numbers less than particular given value of N and not to any specific N2 and (N+1)2. I'm not buying this, and I think it's fairly easy to show that this reflexive notion is false. However, regardless, I will not stay up at night worrying about the theoretical possibility that the vast sea of the asymptotic law of prime number distribution will be divided, in some miraculous fashion, to permit a square gap of a vast magnitude to be prime-free. ("It just ain't gonna happen.") . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Consider the possibility - unlikely as it is - that permitting a proof without perfect precision - might actually matter to some other branch of science? This is, most likely, the weakest argument you will find on this whole page because we all know that science will use math that cannot be proved, when it needs to, with a working assumption that it is true. In fact, the natural sciences and even applied mathematics thrive and prosper on the back of uncertainty. Consider quantum physics! A much stronger argument is that no mathematical proof can be a philosophical proof because of at least three reasons: the theory of supersets, the theory of incompleteness, and the theory of complexity. Since philosophy is not the subject of this article, I will not explain why I choose these three in particular, but I'm not being very original. I recognize the joy of an intellectual pursuit. However, the arcaneness - even alchemy - of the science that is being employed to solve the Landau problems - in particular, the daisy-chaining of obscure dependent theorems, theories, and other conjectures - can never produce an elegant proof that can be appreciated by the rest of us. And that's a sad state affairs because even the most esoteric physics is explicable conceptually to the averagely intelligent and curious. (I'm including general and special relativity, quantum mechanics, the big bang and inflation - but maybe not the Higgs boson :( - in this category.) Even that's not to say that obscurity is necessarily an impediment to popularity: Consider the proof of Fermat's Last Theorem. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
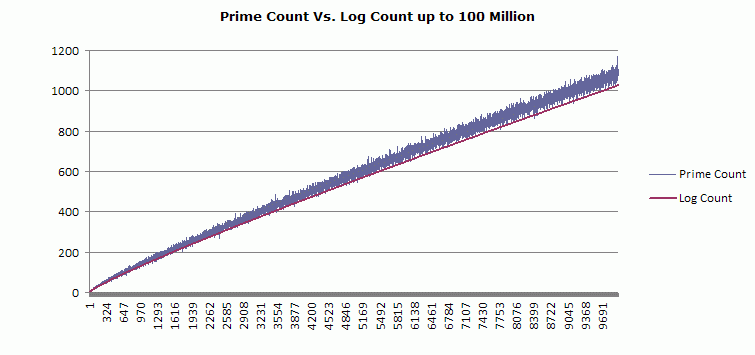
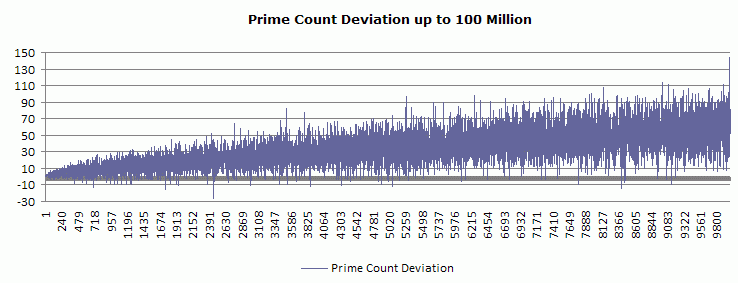
Legendre's Conjecture "There is a prime number between n2 and (n+1)2 for every positive integer n." I will double up on this conjecture with my own: "Of the list of composite numbers between any interval n2 and (n+1)2 there is at least one semiprime 2y and one semiprime 3z?". (I could go further and say the ratio of the real prime count to the quadratic interval is nearly linear, but I'm getting ahead of myself.) Let's step back... The Prime Number Theorem, without any of its elaborations, states: "The number of primes not exceeding x is asymptotic to x/log x." This answers the question: How many primes are there less than the number x? The answer is: Π(x) ~ x/log x, approximately. There is a reason that it's called the prime-counting function - that's how it was originally conceived (see the historical note). What we care about with respect to Legendre's conjecture is not this overall trend, but the prime count, "projected" and real, between every two consecutive perfect squares - and, all-importantly, the proportional deviation between the projected and real counts as the number line progresses.
This question is not secondary to the PNT: It is actually, to my mind, the more important question. This is where I can happily state - without having the faintest knowledge of the existence of the conjecture we are discussing - that I asked and answered this question to my own satisfaction six or seven years ago, writing about it here in complete ignorance of academic number theory - like many other topics you will find on these pages...! A program and results are here: Counting primes by quadratic interval . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Let's break the monotony of this monologue with some light refreshment: Contrast the real prime count with the "PNT-predicted" count *
Left: The real prime count per quadratic interval versus the "asymptotic line". Furthermore, it is graph-able as a line that passes through those intervals, and, empirically, it gets within shooting distance of the discrete real data.. The PNT is a blunt instrument - and I don't like it very much - but it has its uses, whether intended for this purpose or not. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
I pause to note here the historical and ironical fact that Legendre, himself, was the first person to conjecture the size of the prime-counting function, in 1798 to be exact. (There was a revolution on, but he found time.) To quote from the Prime Pages: "The constant 1.08366 was based on his limited table for values of Π(x) (which only went to x = 400,000). In the long run 1 is a better choice..." ( This quote is suspiciously inauthentic though.) This is, in fact, the conjecture that Legendre should be remembered for. And the limit he came up with increases my respect even more. Could the same individual who figured out something that precociously and with such accuracy actually have stated the trite conjecture that became one of Landau's problems? It's not necessary to embark on the journey to infinity, because the arithmetic does not change with magnitude. The growth of the prime count continues to increase to infinity if the PNT continues to infinity. If one is true, the other is also. The delta between the unrefined prime-counting function and the actual prime-counting data is so tiny that it negates the possibility that its deviation could ever come close to challenging Legendre's conjecture. In fact, even entertaining the theoretical possibility of this occurring requires the repudiation of not one but two bedrock principles of mathematical science:
- The evidence: that is the known and observable data. Logically, therefore, one could contend that Legendre's Conjecture does not require its own proof. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
However, to be as clear as possible, there is the reality of an informal "statistical proof" and the high-probability of an arithmetic proof. Legendre's Conjecture is statistically true First, scientists do not use statistical proof as a means to attain certainty, but to falsify claims and explain theory. Second, it conforms to the hypothetic-deductive model or method for defining the scientific method. Third, let me note that nothing I'm saying here is in the least bit original (or well-said for that matter). "It's all out there. Connect the dots." Consider the gap, or interval, between two square numbers, X2 and (X+1)2 strictly as excluding the end-points (that is, the square numbers themselves), its proven empirically (for "small" numbers) and statistically (for "large" numbers) that there can be no cases where the unique prime count is less than two. The prime number theorem states that X / log(X) is a good approximation of the prime-counting function. This can be refined by various methods. However, even in its most unrefined state, for numbers greater than 107 the error terms are tiny in comparison to the ratio of primes to all integers. Given the truth of the prime number theorem, we know that the following formula shows that the prime count, within an error term, increases over successive quadratic intervals to infinity if PNT is correct.
This is not a matter of dispute. The absolute prime count growth will continue if you plug in any number for which it is computationally possible to use the natural logarithm. It is not necessary to invoke the Riemann Hypothesis to refine the error term. because the growth of the prime number count dwarfs it. For "small" numbers the empirical computed data is a piece of cake (my generated data < 108). For "large" numbers, we can use data that uses raw computational horsepower up to 1025 at present. Beyond this, we have rigorous proofs that use analytical continuation without the RH. The real error term is far smaller than any deviation that could negate the effect of quadratic growth. For any computed magnitude greater than, say, 1010 the largest negative deviations are a fraction of one percentage point of the asymptotic line. That's it: A statistical proof that "There is a prime number - in fact, at least two - between n2 and (n+1)2 for every positive integer n" without a single statistic. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
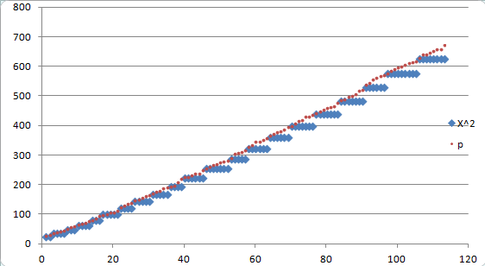
Two more pictures... In the beginning, the real prime count expansion establishes a near-linear-ratio growth pattern with the square interval count (as projected by the PNT-derived interval count formula).
Left: A tiny plot of the early prime expansion. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Spinning up the data "A Resplendent Rule" "The Rule of 2 and 3": Two demonstrations
This particular Landau problem is true until proven false (which it simply cannot be). . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Monty Hall Problem for Dummies No other mathematical puzzle
has produced more heated arguments and more
misunderstanding than the Monty Hall Problem.
It's tempting to call it deceptively simple, but
the truth is it's deceptively complex. In fact,
I can simplify its essence to one question: If
you were handed two decks of cards, one with
2/3 aces and the other with 2/3 jokers, and
were asked to pick an ace, from which pack
would you draw the card? If
that is not a sufficient clue, you need to
read this. . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
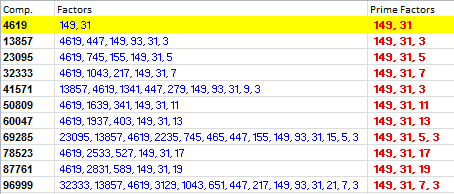
Factor Families A factor family is a set of composites that share common factors. The family begins with a semiprime, and all members of the set share the two prime factors of the semiprime. The family can be extended indefinitely. For example, for the first 100,000 odd composites the factor family of 4619 (149*31) looks like this:
There are a few things to note about this representation: The prime factors (in red) are distinct, so, for example, 3 can be 3*3 or 3*3*3, and so on. The complete factors (nonprime and prime in blue) of each composite all have three common factors: the semiprime and its prime factors. By definition, a semiprime cannot have nonprime factors. Download Excel worksheet: Factor Families (1.5MB) . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Modal Distribution of
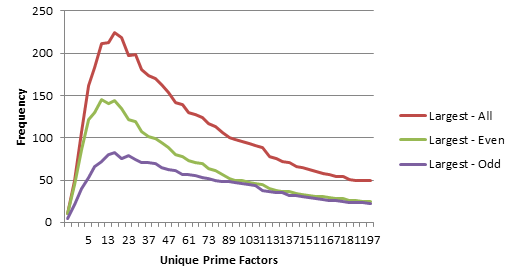
Distinct Prime Factors: Yes, you can find the answers to life's most persistent questions here! What is the cumulative distribution of distinct prime factors? The answer is both what you were expecting and more than you were expecting. As expected, the cumulative frequency of unique prime factors diminishes with size, so that 2 is the most frequent factor, 3 is the second-most frequent factor, 5 the third, and so on for all prime factors. However, it turns out that the cumulative frequency of the largest prime factors - the biggest factor of each composite - has a modal distribution that is increasing at a slow rate approximating the cube root of N. Up to 10,000, this mode is 19. Up to 1,000,000, this mode is 73. It's fairly safe to assume that if we graph any given set of numbers, there will be a distinctive peak near P^3 = N.
Distribution of the
largest prime factor for each composite less
than 10,000. (The difference Download Excel
worksheet: Distinct Factor Analysis
(macro-enabled) (30KB) . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Paired, Squared, Cubed, and Primed...? If we pick a square or a cube and count up to the nearest prime number, what are the odds that a prime number will also exist if we count up by the same amount from its root? The answer, it turns out, is surprisingly high - and even higher for cubes than for squares. If the question sounds confusing, it's easy to illustrate: Squared example:
Cubed example:
The results are:
Download CSV files: Squared-1000 (30KB) and Cubed-1000 (35KB)
Download CSV files: Squared-10000 (351KB) and Cubed-10000 (425KB) . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
What has 6
got to do with it?
Did you know? The difference between the first and fourth product of a quadratic polynomial - including proximate-prime polynomials - is always a multiple of 6. This divisibility by 6 does not stop with the fourth term. It recurs with the polynomial's 7th term, 10th term, 13th term, and so on ad infinitum. For example:
A whole new meaning for "sexy primes"...? Lots more data available: PPPs < 50000, t1 - t15 ("T" denotes each t value divisible by 6) Download (115KB) . . . .
. . . . . .
. . . . . .
. . . . . .
. . . . . .
Factoring in Polynomial Time: A Pronic Solution... Sometimes the best things in life are free - well, almost free... and very simple... and blindingly obvious. A single GCD calculation using the closest pronic number to N will produce a factor for one-third of composites not divisible by 2 or 5 up to any size. For example, the nearest pronic to 898097881 is 898110992, and these numbers share a GCD of 1873 - a prime factor of both numbers. An analysis of N < 10,000,000 shows that 35.8% of the nonobvious composites are factorable with a single GCD calculation. What is the common characteristic of this huge class of numbers? They appear to conform to rational angles in the Sacks number spiral. Such numbers can be generated with RadiusTest using the Lines option and produce polynomials with a third coefficient of 0. Expanding the GCD calculation to pronic numbers within 6 quadratic intervals of N provides a nearly instantaneous factorization test for more than two-thirds of composites ending in 1, 3, 7, or 9 regardless of magnitude. Here is an analysis of composites less than 107 with GCDs calculated for pronics from 6 quadratic intervals less than N through 6 quadratic intervals greater than N. It shows a 74.4% success rate. Analysis for N<107 Download (11MB) Previous
Articles |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Tools for Testing Natural Numbers |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| MinusSquare | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Miller-Rabin | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FermaticTest | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| QTest | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| RadiusTest | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ZetaTest | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| PrimeTest | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Recommended sites: