without imaginary numbers
First published Feb 02
Last updated Feb 13, 2008
Now in Sloane's:
OEIS Sequence A134969
This topic is continued and partially superseded by
Q-Paired Primes: The Investigation Continues...
Biquadratic Paired Primes up to 100,000 in CSV format:
-1st Prime
-2nd Prime
-1st Perfect Square
-2nd Perfect Square
-Offset
-Product
Download (101KB)
What Are Odd Squared, or Biquadratic, Paired Primes? |
||||||||||||||||||||||||||||||||||||||||||||||||||||
| I would like to call the subject of this page Biquadratic Paired Primes (BQPPs). However, since biquadratic is another term for quartic, or fourth degree polynomials, I am being cautious about it. (Well. like biweekly, it could be fairly used to mean two completely different things....)
The sense in which I'm using biquadratic is the sense of every other quadratic interval: in fact, a span that bridges one complete interval and two partial intervals. Odd Squared Paired Primes is not entirely accurate either, as odd square implies the odd perfect squares only. In fact, the pairs of primes I'm going to describe can span two odd perfect squares (with an even one between) or two even perfect squares (with an odd one between). A simple definition would be this:
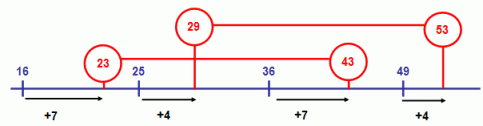
The following diagram illustrates the relationship for two pairs of biquadratic primes:
In this example, 7 and 19 are offset by 3 from the even perfect squares 4 and 16:
Another odd-offset one: 71 and 107 are offset by 7 from 64 and 100:
The even offsets work the same way, but from the odd perfect squares. For example, 97 and 137 are offset by 16 from 81 and 121:
In some sense, these paired primes may be related to twin primes. That's pure conjecture, just an impression based on looking at their frequent co-location. In these examples, one or both paired primes are also twin primes:
As you can see, paired primes are the rule rather than the exception at the beginning of the number line. There are 32 primes, up to and including 137 - and 24 of them are paired. So which prime numbers less than 137 are not paired?
After the high-density start, the numbers fall off steeply - in fact, there are just 25 more pair-participating primes up to 1,000. That's 49 paired primes out of 168 primes altogether (about 30%). By 100,000, it appears that 1,895 of the 9,592 primes are paired. That's about 20%. It seems that the first prime of every biquadratic pair is less than the second prime of the preceding pair. In other words, the pairs appear consistently to overlap. This tandem or relay relationship is shown here (and in the illustration above).
I haven't looked that hard for an exception yet. There may well be exceptions in the prime pairs under 100,000 if you care to look at this text file (101KB). (You could actually extend this claim to the first pair, 3 and 11, if you are willing to shed your inhibitions and allow 0 to be a perfect square and, dare I say, pretend 1 is a prime... confusing since it's a perfect square also... OK let's just forget that.) There may be a PhD awaiting a mathematician here.... A pronic number is near the heart of every biquadratic pair. Notice that the "midpoint" in the paired prime examples, occupying the intermediate quadratic interval, was a pronic number in the first example (3*3+3 = 12). This will only occur when the offset equals the root of the pronic number. So, for example if the offset is 7, the pronic would have to be 56 (7*7+7). I think the following additional assertions can be made about biquadratic pairs and pronic numbers:
Speculatively, The number of quadratic intervals that occur before a relative pronic number (the paired-prime difference in point 2) occurs appears to increase by a finite difference of 1. I would love to be able to say that every absolute pronic number has a BQPP, but this is not the case. About 1 in 5 do not, and this frequency of non-BQPP pronics gradually increases.
The products of BQPPs could be called "odd squared composites". Interestingly, they bear a passing resemblance to primes - although they are mostly not pseudoprimes. (FLT correctly identifies most of them to be composites.) The resemblance is the superficial one that the last digit is always 1, 3, 7, or 9. There is one single exception to this - 85, the product of the second prime pair (comprising 5, of course, and 17). For what it's worth, these composites are the squared median of the primes minus 2 plus the offset multiplied by 4. If you have something against straight multiplication, you can arrive at the answer this way:
Now this suggests doing a reverse calculation from any given number - a trivial calculation for even very large numbers - as an initial step in factoring it, to see if it belongs to this sizeable class of composites. You would do it like this: Say you've been given a big number that looks like it might be a prime - that is, it ends in 1, 3, 7, or 9. (You can pretend that it's much bigger than this one if you would like.)
You would proceed as follows:
Now you need to determine the perfect squares that straddle 937123. The easiest way to do this is to find its square root - or the quartic root of N (also called the biquadratic root... yes, I can use this term without guilt!).
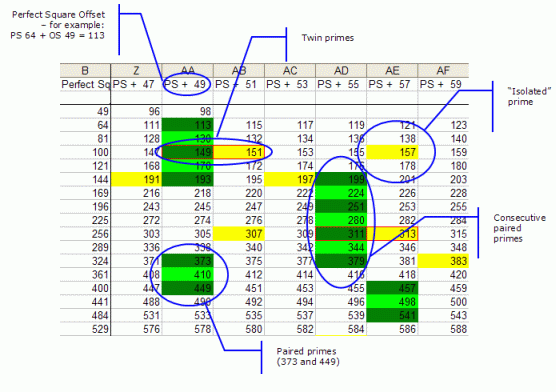
We have shown that a large number N that is potentially a prime is in fact a composite of biquadratic paired primes. However, this is not a proof unless the factors are prime factors. Unfortunately, this procedure does not prove that. Try a demonstration of the "algorithm", exactly as described, in JavaScript. Biquadratic paired primes can be easily visualized using a grid with an axis of perfect squares and an axis of offsets from the perfect squares. The following illustrates the most salient points. You can generate this in Excel using the VBA code below. Notes:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|