Composites  
 
    home
                   
Lists of Composites

with Prime Factors


Download or view in your browser

Primes

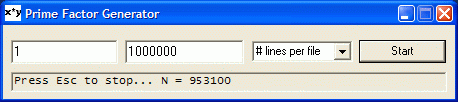
Perfect Squares

First 100

1 - 133  (2KB)

First 1,000

1 - 1,197  (20KB)

First 10,000

1 - 11,374  (217KB)

First 100,000

1 - 110,487 (2.5MB)

First 1,000,000

1 - 1,084,605 (6.5MB - zip download only)

 

Want More Prime Factors...?

Generate prime factors for numbers up to 10^15.

Download (13KB)

Want Distinct Prime Factors Only...?

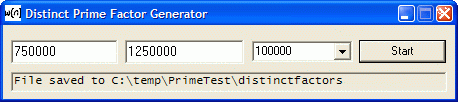
Generate distinct prime factors only. For each N, each prime factor is listed once.

Download (14KB)

For example, the complete prime factorization of 1000000 is:

2 * 2 * 2 * 2 * 2 * 2 * 5 * 5 * 5 * 5 * 5 * 5

The distinct prime factors are 2 and 5, and the number of distinct factors is 2.

The number of distinct prime factors is the subject of the Erdős–Kac theorem. They are denoted ω(n). So ω(1000000) = 2.