intelligence of the numberverse
home

The compass points are a convenient way to understand orientation in the spiral. Direction in the spiral has particular significance because it determines the distribution of every number in the spiral. If you know a number, you know its location.
The hemispheres of the spiral can be called north, south, east, and west, while the quadrants of the spiral are northeast, northwest, southwest, southeast. (The use of geographic terms is purely for ease of understanding and is not meant to infer any deeper significance.) None of the axes are straight lines, but are actually slightly curved. Their position on the number line is what determines their position in the spiral.
East
The spiral begins and completes each rotation on the designated "0°" axis. The numbers on this axis are the perfect squares, so the formula is simply:
n^2
The sequence begins: 1, 4, 9, 16, 25, 36.
North
Due north represents a quarter turn of the spiral. The
formula that describes the numbers on this approximately 90° axis is:
n(4n+1)
The sequence begins: 5, 18, 39, 68, 105, 150.
West
Due west represents a half-turn of the spiral. The numbers on this approximately 180° axis are the pronic numbers (see below):
n(n+1)
The sequence begins: 2, 6, 12, 20, 30, 42.
South
Due south represents a quarter turn of the spiral. The
formula that describes all numbers on this approximately 270° axis is:
n(4n-1)
The sequence begins: 3, 14, 33, 60, 95, 138.
(The reason that the north and south progressions grow at twice the rate of the east and west progressions is that each north/south number is separated by two turns of the spiral.)
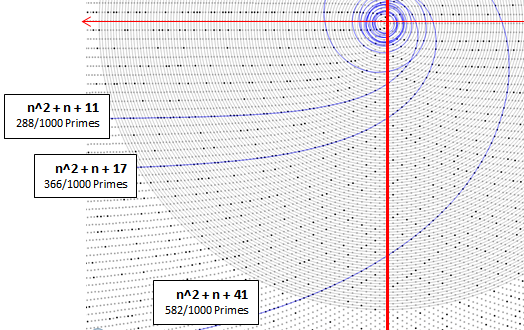
The so-called pronic numbers are of particular significance in the spiral because the curves that are derived from the pronic formula with a positive or negative constant produce statistically and predictably more prime numbers than other curves.
The pronic number are simply those formed by multiplying an integer by itself-plus-one. Thus the formula is n(n+1), and the first few examples are:
1(1+1)=2
2(2+1)=6
3(3+1)=12
4(4+1)=20
5(5+1)=30
6(6+1)=42
In terms of the Sacks Number Spiral, the westbound equatorial line is comprised solely of pronic numbers as illustrated.
![]()
Product curves are polynomials conforming to one of the equations given above. For example, n^2 - n + 41 is a pronic curve.
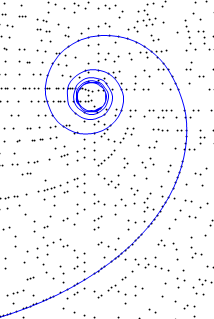
After circling the center of the spiral, westbound "P" curves flatten out and run parallel to the pronic axis, eastbound "S" curves flatten out and run parallel to the square axis.
Both aspects of product curves' behavior have strikingly simple explanations that were identified by Sacks.
Number of rotations
This is determined by the offset rule, which states: "A single rule determines the number of rotations for both even and odd curves: the number of revolutions is equal to the average of the offset's squarest integral factors. For example, the curve with offset 12 makes 3.5 rotations, and 3.5 is the average of 3 and 4, the squarest factors of 12." (Robert Sacks)
Horizontal alignment
In the spiral, east is a zero turn, north is a quarter turn, west is a half turn, and south is a three-quarter turn. 0 represents the point of origin for a rotations and 1/2 represents the halfway point in the rotation.
- The square root of n^2 is n.
So the fractional part of eastbound curves approaches 0.
- The square root of n(n+1) is n.5
So the fractional part of westbound curves approaches 1/2.
You can test this fact in RadiusTest with any square (eastbound) or pronic (westbound) curve.
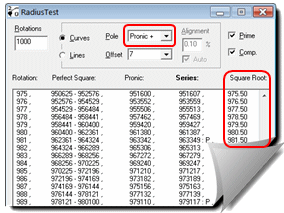
This example illustrates that the fractional part of the square root of a pronic curve approaches one-half once the curve aligns with the pronic axis.
The constant part of the polynomial (+ or - C) becomes less and less significant as the value of N increases. As the effect of the constant becomes more and more negligible, so does the curve more and more closely approximate the straight line defined by the square root or pronic number progression.
 |
Symmetry and Asymmetry in the Number Spiral: See the Numbers: By Density and By Ratios |
| The Sacks Number Spiral | |
In 1994, Robert Sacks, a software engineer, devised an original method for representing the classical number line of positive integers. He published his findings on the web in 2003. In this method, an Archimedean spiral centered on zero and making one counterclockwise rotation for each perfect square produces a remarkably organized distribution of prime and composite numbers. In some respects, this 2-dimensional "number sphere" can be thought of as a periodic table of numbers - because of the orderly patterns and progressions it reveals. The Sacks Number Spiral is both visually arresting and intellectually compelling. It seems likely that it can provide deeper insights into prime number patterns than the well-known Ulam spiral because, in effect, it joins together the broken lines of Stanislaw Ulam's pseudo-spiral. Sacks' work has focused on product curves, lines that originate from the spiral's center, or near to it - and traverse the spiral's arms at varying angles. His graphing demonstrates that there are multiple orderly factor and prime number progressions. Since the spiral can be extended outward infinitely, the product curves themselves may be considered infinite also. It's an open question whether or not the spiral has any predictive value. For example, can the number spiral's product curves be used to predict the decomposition of very large numbers into prime factors?
Like the Cartesian plane and the Complex plane, the number spiral represents a plane in which points can occupy one location only. Unlike the traditional planes, all numbers are natural numbers: the positive integers. (However, a spiral of negative integers with negative perfect squares can be visualized as sharing the zero-point center and rotating clockwise in a parallel plane. This is conceptually useful because many polynomial sequences begin with negative integers, then enter the positive spiral, before returning to the negative region.) Quite unlike the Cartesian and Complex planes, the Spiral plane does not require a coordinate system to identify a point. It is a unipolar positioning system. Just knowing the number reveals its location in the spiral - its position relative to every other number in the spiral, its distance from the previous and the next perfect squares, and, potentially, all the curves it can occupy relative to other numbers in the spiral: its polynomial classification. The parabolic curve is a well-known attribute of polynomial equations in classical algebra. In fact, solving the roots of a polynomial means finding the points along the X axis of the Cartesian plane that the parabola intersects. So curviness appears to be rooted in mathematical axioms, but is shown in a new light by the Spiral plane. The fact that the roots of many polynomials, even simple ones, cannot be solved in the Cartesian plane – that is, they do not intersect with the X axis – is one of the intellectual justifications for the Complex plane and Complex numbers. Underlying the distribution of numbers in the spiral plane is the alignment of perfect squares. The progression of perfect squares determines the expansion of the spiral. The first complete rotation of the spiral necessarily comprises three poles - 1, 2, and 3 (a perfect square and two primes). However, the spiral, taken as a whole, aligns along four axes, which can be designated, for convenience, as north, south, west, and east. Zero degrees (aligned due east in the Sacks spiral) is the primary axis and corresponds with the perfect squares: 1 (1*1), 4 (2*2), 9 (3*3), 16 (4*4), 25 (5*5), and so on. Due west is the axis of pronic numbers, with the progression 2 (1*1+1), 6 (2*2+2), 12 (3*3+3), 20 (4*4+4), 30 (5*5+5), and so on. Polynomial sequences that comprise a pronic number are the number progressions that are by far the richest in prime numbers. The plus or minus sign of the polynomial's constant determines whether the path of the curve lies before or after the spiral crosses the east-west axis. The constant is simply an offset quantity from the basic formula: n^2 for east, n(n+1) for west. For example, a curve that is -17 occurs either before the spiral crosses the pronic axis or before the spiral crosses the square axis. Hence a negative-constant curve can occupy the northwest or southeast quadrant of the spiral.
One of the most striking aspects of the Sacks Number Spiral is the predominance of major prime curves in the western hemisphere (opposing side from the perfect squares). For example, one of those curves, heading southwest, contains the numbers of the form n(n - 1) + 41, which is a famous prime-generating formula discovered by Leonhard Euler in 1774. In the number spiral, Sacks is able to make the striking assertion that a prime number is "a positive integer that lies on only one product curve."
Elsewhere on this site, these curves have been termed "proximate-prime polynomials". They are simply 2nd-degree polynomials that can be described by four consecutive primes (such as 41, 43, 47, and 53, the first four integers of Euler's sequence). A significant proportion of such polynomials (46 of the first 333) have greater than 50% prime values in the first 1,000 numbers of the series.
Product Curves and Polynomials Sacks describes product curves as representing "products of factors with a fixed difference between them". In other words, every curve can be represented by a quadratic equation - a second-degree polynomial - no coincidence given the primacy of the perfect square in the structure of the spiral. Curves can be almost straight but, more typically, perform partial, complete, or multiple clockwise revolutions - counter to the spiral itself - around the origin before straightening out at a particular offset from the east-west axis. The number of revolutions is the direct product of the offset. The greater the offset, the greater the number of revolutions a curve must make before pulling free from its initial "orbit". This relationship is formalized in the Sacks Offset Rule. Product curves can contain composites or primes, the relative proportion of each being predicated on the all-important offset. Simple observation shows that curves with prime number offsets are reliably richer in primes than other odd-number composite offsets. This observation is the basis for the work on this site related to proximate-prime polynomials. Why do the curves straighten out anyway? It turns out the answer is quite simple and has to do with how polynomials are related to perfect squares. A polynomial curve straightens out when its values align with perfect squares or the median values of perfect squares. The point at which a polynomial curve aligns with the horizontal axis is entirely predicated on the third coefficient of a 2nd-degree polynomial equation. A product curve for a given polynomial (of type n² +/- n + x, where x is the offset) travels clockwise, counter to the spiral itself, before intersecting with the squared value of the offset number on the spiral. This is the point of pronic alignment. An offset of 41 literally means the curve will align with the pronic axis at 41*41 - the composite number 1681. From that point forward, the curve is aligned with the pronic axis. (See Polynomial Pronic Alignment.) Is the curvy portion of a curve different somehow than the (infinite) straight portion? Certainly the greatest concentration of primes for many polynomials occurs within the pre-alignment portion of their paths across the number spiral.
Michael M. Ross |
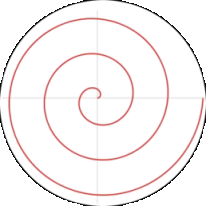
The spiral, which is termed Archimedean, originates from the center and rotates counterclockwise starting and completing each rotation with due east. This axis is generally designated as 0°.
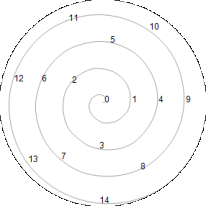
The number line is superimposed on the spiral, and it contains every counting number, beginning with 0, which is the center of the spiral. 1 is the unit of the number line and the number spiral.
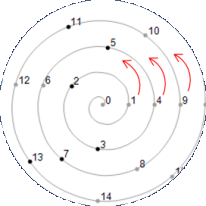
Each counterclockwise revolution of the spiral begins with a perfect square: 1, 4, 9, 16, and so on.
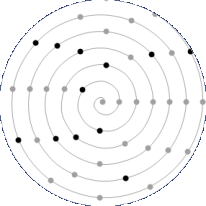
The spiral's product curves are revealed by showing prime and composite dots with different shades or sizes.
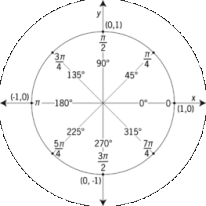
Another way to think about the spiral is as a "unit circle". In the unit circle you can see the degrees of the circle begin with "due east", just as the spiral does - and that this is 0°. In the unit circle, every position is shown as some fraction of the simple XY coordinate system. (This diagram also shows fractions of Pi, each segment being 2 radians - another way to divide a circle.)
Every number on the spiral plane has an equivalent XY coordinate in the unit circle. Since the unit circle can exist in the Z, or complex plane, it is possible that the number spiral can be used to bridge the theory of prime number distribution for real numbers (namely, the Prime Number Theorem) and complex numbers (namely, the Riemann Hypothesis). Of particular interest is the fact that curves with the highest prime density follow the -1,0 coordinate. The Riemann hypothesis for curves over finite fields states that the roots of a projective line have an absolute value q - 1/2.
Most images on this page were generated with Vortex: © 2007 Robert Sacks
For more illustrations of the Sacks Number Spiral and to explore the spiral yourself, with Vortex, go to NumberSpiral.com
Also see Number Spirals
Related Articles